GLART week 3: Space (Perspective, Ortho, Frustum)
OpenGL provides several functions to define the dimensions of the viewable
space of a scene. These functions create projection matrices that define the
"viewing volume" of the scene: what area of the scene will be rendered. Any
geometry outside of the viewing volume is "clipped": it is not rendered.
We have already worked with gluLookat() which defines where the eye is placed
relative to the geometry in the scene, and works with the ModelView matrix. If
we think of gluLookat() as the camera position, then gluPerspective() is the camera
lens.
gluPerspective() is in the GLU utility class and provides a simple way to
specify the depth and field of view (FOV) of your scene. Using the analogy of a
camera lens, gluPerspective() defines how wide or narrow the view is, ie.
are we using a wide-angle lens or a telephoto lens, and what it the depth-of-field of
the scene.
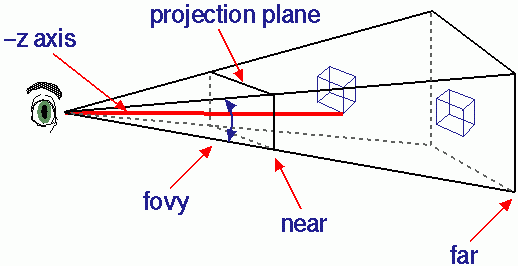- a small field of view (15) is like a telephoto lens
- a large field of view (150) is like a wide angle lens
- the near and far values determine how deep the scene is
gluPerspective() works with the Projection matrix. In the rendering process, the
3D geometry of the scene is mathematically "projected" onto the 2D space of the
screen. The projection matrix determines how this projection occurs.
The gluPerspective() command is not actually a core OpenGL function, it is a utility
function (hence the prefix "glu") that calls a lower level OpenGL function: glFrustum().
A frustum looks like a section of a pyramid and the glFrustum() function creates a
matrix that defines a frustum shaped space. This lower level function provides greater
control over the projection matrix, though is less intuitive than the gluPerspective()
function.
OpenGL can also create spaces with no perspective at all. The glOrtho()
command "flattens out" the space, creating an orthographic projection,
like a blueprint. In this case, the Z position of a shape has no
effect on it's size or position on screen. This is not literally a
two dimensional space though. The scene still has Z coordinates and
objects can be in front of one another, but they will be rendered
without perspective.
glOrtho() also can be used to exactly map the scene space to the
pixel dimensions of the screen. For instance you can use glOrtho()
to define a scene that is 800 units wide and 600 units high.
When shown on a screen that is 800x600 pixels, a vertex at position
100,200 will appear at pixel position 100,200 on screen.
With glViewport() you can define what rectangular part of the
screen to render the scene into. By default the viewport is the same
size as the window itself, so in most cases you don't have to do anything.
At times you may want to render into a specific area of a window and
glViewport() allows you to define the bounds of that area. It is
important to match the aspect-ratio of the scene that you used in
gluPerspective(), glFrustum(), or glOrtho() with the aspect ratio
of the viewport. If you define a viewing space with a 3x4 aspect
ratio, but set the viewport to a widescreen ratio such as 16x9, your
scene will appear squashed on the screen.
Here is a summary of the Geometry Transformation Pipeline.
Assigment:
Space, Perspective and Ortho
Reading:
Redbook pages 96-104 "Overview: the Camera Analogy" (Chapter 3)
Redbook pages 116-130 "Viewing Transformations" (Chapter 3)
Redbook pages 177-180 "Real World and OpenGL Lighting" -- a brief intro to light
Examples:
GLART_3_city.java Perspective and Orthogonal view of a cityscape
GLART_3_city_viewports.java Cityscape drawn in two Viewports using glOrtho() and glFrustum()
GLART_3_blackboard.java Use Ortho to exactly match screen coords to the world
You'll need this image for the cityscapes (save into the images folder in your project)
Ideas:
The Invention and Re-Invention of space
See also:
nate robbins projection tutorial:
http://www.xmission.com/~nate/tutors.html
opengl FAQ -- Viewing and Camera Transforms
http://www.opengl.org/resources/faq/technical/viewing.htm
Principles of Perspective
http://www.webexhibits.org/sciartperspective
http://www.webexhibits.org/sciartperspective/tylerperspective.html
Speculations on the origin of Linear Perspective, by Richard Talbot
http://www.nexusjournal.com/Talbot-pt01.html
Interesting article discusses some early techniques in perspective rendering.
"... Masaccio's Trinity, (circa 1427), which is thought to be the earliest painting
to show a systematic approach to spatial diminution, and Piero della Francesca's
Flagellation. These paintings are considered to be particularly significant because
of the artists' respective links with Brunelleschi, credited with discovering perspective,
and Alberti, credited with the first written account of the theory of linear perspective
in 1435."
NOTES:
-----------------------------------------------------------------------
glMatrixMode(GL_PROJECTION)
call GL11.glMatrixMode(GL11.GL_PROJECTION) to switch to the projection matrix
before calling gluPerspective(), glFrustum() or glOrtho(). These three
functions each create a matrix and multiply the current matrix by it.
Remember to switch back to the Modelview matrix (glMatrixMode(GL11.GL_MODELVIEW))
before calling gluLookat() or doing any transformations on your geometry.
GLU.gluPerspective( fieldOfView, aspectRatio, nearZplane, farZplane )
Use gluPerspective() to define the viewing space. Think of this as the type
of lens on a camera:
- a wide-angle lens has a bigger field of view (ie. 150 degrees)
- a telephoto lens has a narrower field of view (ie. 15 degrees).
- fieldOfView is an angle that sets how wide the view will be
- aspectRatio sets the shape of the rendered scene. It should
be the same shape as your viewport or the scene will appear
stretched or squashed.
- nearZplane, farZplane are like the focal distance of a camera,
if nearZ is 1 and farZ is 10 then the camera can only see
things between one foot and 10 feet in front of it. All
geometry outside that range will be "clipped" (will not
be rendered)
NOTE: The nearZplane and farZplane are NOT Z coordinates in the world,
They are distances from the eye position.
glFrustum(leftX, rightX,
bottomY, topY,
nearZ, farZ)
Defines a "frustum", a perspective viewing space.
gluPerspective() is a higher level function that calls glFrustum()
to create the appropriate projection matrix. glFrustum() can be
used in situations where you need more direct control of the
viewing space.
glOrtho(leftX, rightX,
bottomY, topY,
nearZ, farZ)
Defines an orthographic viewing space, meaning a space that has no
perspective. This is not literally a two dimensional space. The
geometry may still have Z coordinates and objects can move in front
of other objects, but parallel lines in the scene will not converge
as they recede from the viewpoint.
glViewport(x, y, width, length)
Sets the position and dimensions of the OpenGL "screen". By default
the viewport is the same dimensions as the window. The glViewport()
command can be called to render into a smaller area of the window if
desired. Remember that the aspect ratio (width / height) of the
viewport should be the same as the aspect ratio used in gluPerspective(),
glFrustum() or glOrtho().